Before knowing about eccentricity, you must know about the conic sections. The intersection of a cone with the plane results in the formation of a curve known as Conic sections. The eccentricity can be defined as the curve of any shape which characterizes the shape. This characterization is done irrespective and regardless of the given size of a shape.
There are various curves that are formed when the cone (double-napped) strikes or intersects with the plane. Some of the curves are as follows hyperbola, circle, parabola, and ellipse. A circle can be defined as a geometrical shape with no curves.
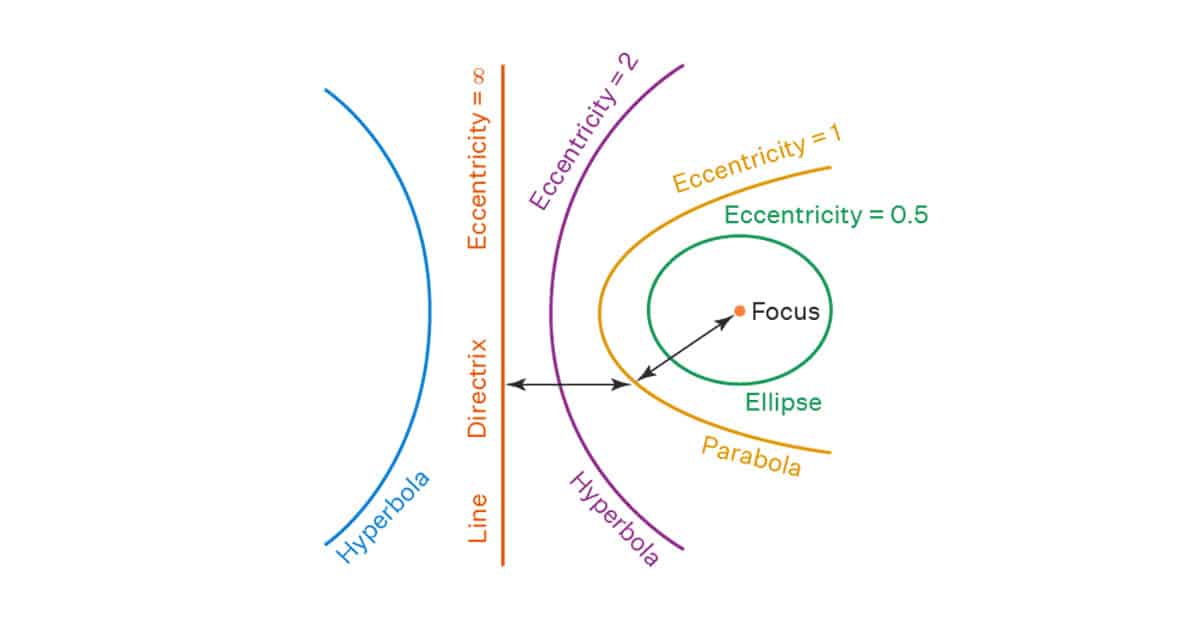
A plane curve that is symmetrical as a mirror and is portrayed in the shape of the letter ‘U’ can be defined as the parabola. An ellipse is almost identical to a circle, but it is flatter than a circle. In this article, we may cover and discuss some topics related to conic sections such as what is a hyperbola, terms related to a hyperbola, and some apps, locations related to it.
What is a Hyperbola?
In the previous section, we dealt with the conic sections and their various types. One of the types of Conic sections is a hyperbola. It can be defined as a smooth curve that is formed with the help of different parts or components such as FCI, major and minor axis, center, and many more. A hyperbola is also formed when two different cones interest or strike with the plane.
Hyperbolas are always symmetrical to the conjugate axis and are kind of similar to an ellipse. There are various concepts such as eccentricity, foci, latus of the rectum, and many more that are connected to a hyperbola. . The eccentricity can be defined as the curve of any shape which characterizes the shape irrespective of its given size. The latus rectum is also known as the semi latus rectus is regarded as the type of conic section that passes and crosses through the focus.
Some Important Terms Related to a Hyperbola
As mentioned above, a hyperbola can be defined as a smooth curve that is formed with the help of different parts or components such as foci, major and minor axis, and so on. Hyperbolas are used in our everyday life extensively. The following points analyze the significant terms related to a hyperbola :
- A point that is used to construct a conic section can be defined as the focus of hyperbola. There are two focuses of a hyperbola and thus named as foci of hyperbola.
- A point where the foci of hyperbola meet and join can be regarded as the midpoint of a hyperbola.
- The length of the hyperbola whose units are equivalent to 2a units is known as the major axis. Similarly, the length of the hyperbola whose units are equivalent to 2b units is known as the minor axis.
- A point where the hyperbola meets with the axis is defined as the vertices of the hyperbola. The axis is the highest point.
- The straight lines that pass through the focus ( two ) and the midpoint which is known as the center is regarded as the transverse axis of the hyperbola. Similarly, a line that passes through the center and is perpendicular ( 90 degrees ) to the transverse axis is defined as the conjugate axis.
Some Applications of Hyperbola in Everyday Life
Some of the applications of hyperbola in day to day life are mentioned below:
- Hyperbolas are generally used to design a bridge. One example is the bridge in Japan which was made with the help of a hyperbola.
- It is considered to be the basis of solving a problem based on Trilateration.
If you want to study eccentricity and hyperbola in a detailed, fun, and interactive manner, visit Cuemath.
